去年刚挂的科,重修时为努力复习所写的提纲,不说了,大学数学一生黑
Head Pic: 【Fate/GrandOrder】「何だかんだ仲がいい」/「翠月 琉」のイラスト [pixiv]
常微分
第一章 绪论
$\displaystyle\large{ \int 0dx=C\\ \int 1dx=x+C\\ \int x^adx=\frac{x^{a+1}}{a+1}+C\ (a\ne-1,x>0)\\ \int\frac1xdx=\ln|x|+C\\ \int a^xdx=\frac{a^x}{\ln a}+C\ (a>0,a\ne1)\\ \int\cos axdx=\frac1a\sin ax+C\ (a\ne0)\\ \int\sin axdx=-\frac1a\cos ax+C\ (a\ne0)\\ \int\frac{dx}{\sqrt{1-x^2}}=\arcsin x+C=-\arccos x+C'\\ \int\frac{dx}{1+x^2}=\arctan x+C=-\mathrm{\,arccot\,}x+C'}$
第二章 一阶微分方程的初等解法
2.1 变量分离方程与变量变换
- 可以直接变量分离的 $\displaystyle\frac{dy}{dx}=f(x)g(y)$
- 齐次方程 $\displaystyle\frac{dy}{dx}=g(\frac{y}{x})$,用变量代换将其转变为变量分离方程
-
分式线性方程 $\displaystyle\frac{dy}{dx}=\frac{a_1x+b_1y+c_1}{a_2x+b_2y+c_2}$
-
如果 $\displaystyle\frac{a_1}{a_2}=\frac{b_1}{b_2}=k$,则用变量代换转变为变量分离方程
- 否则先联立求解 $\begin{cases}a_1x+b_1y+c_1=0\\a_2x+b_2y+c_2=0\end{cases}$,再代换 $\begin{cases}X=x-\alpha\\Y=y-\beta\end{cases}$,即可化为齐次方程
-
2.2 线性方程与常数变易法
-
齐次线性方程 $\displaystyle\frac{dy}{dx}=P(x)y$ 直接变量分离得通解 $\large{y=ce^{\int{P(x)dx}}}$
-
非齐次线性方程 $\displaystyle\frac{dy}{dx}=P(x)y+Q(x)$
-
先求得齐次解 $\large{y=ce^{\int{P(x)dx}}}$,然后假设有形式解 $\large{y=c(x)e^{\int{P(x)dx}}}$,并带回原式解出 $c(x)$
- 直接通解公式 $\large{y=e^{\int{P(x)dx}}(\int{Q(x)e^{-\int{P(x)dx}}dx+\widetilde{c}})}$
-
- 伯努利方程 $\displaystyle\frac{dy}{dx}=P(x)y+Q(x)y^n\ (n\ne0,1)$
- 将方程各项乘以 $y^{-n}$,然后令 $z=y^{1-n}$,则 $\displaystyle\frac{dz}{dx}=(1-n)P(x)z+(1-n)Q(x)$
- 直接通解公式 $\large{y^{1-n}=e^{\int{(1-n)P(x)dx}}(\int{(1-n)Q(x)e^{-\int{(1-n)P(x)dx}}dx+\widetilde{c}})}$
2.3 恰当方程与积分因子
恰当方程
将一阶微分方程写成对称形式 $M(x,y)dx+N(x,y)dy=0$
如果此时有 $\displaystyle\frac{\partial{M}}{\partial{y}}=\frac{\partial{N}}{\partial{x}}$,则该方程为恰当方程,并且可以表示为某函数 $u(x,y)$ 的全微分 $M(x,y)dx+N(x,y)dy \equiv du(x,y)$,通解为 $u(x,y)=c$
通解公式 $\displaystyle u=\int{M(x,y)\partial{x}}+\int{[N(x,y)-\frac{\partial}{\partial{y}}\int{M(x,y)\partial{x}}]dy}$
积分因子
如果存在非零连续可微函数 $\mu(x,y)$ 使得 $\mu(x,y)M(x,y)dx+\mu(x,y)N(x,y)dy=0$ 为恰当方程,则称 $\mu(x,y)$ 是方程的一个积分因子,此时可按照恰当方程来求解
- 观察法:利用已知的或熟悉的微分式的原函数求积分因子
- 公式法:积分因子必定满足 $\displaystyle\frac{\partial(\mu M)}{\partial{y}}=\frac{\partial(\mu N)}{\partial{x}}$
- 如果积分因子只与 $x$ 有关 $\displaystyle\frac{1}{N}(\frac{\partial{M}}{\partial{y}}-\frac{\partial{N}}{\partial{x}})=\varphi(x)$,此时 $\large\mu(x,y)=e^{\int{\varphi(x)dx}}$
- 如果积分因子只与 $y$ 有关 $\displaystyle-\frac{1}{M}(\frac{\partial{M}}{\partial{y}}-\frac{\partial{N}}{\partial{x}})=\psi(y)$,此时 $\large\mu(x,y)=e^{\int{\psi(y)dy}}$
- 分组组合法
2.4 一阶隐式微分方程及其参数表示
能解出 y 或 x 的方程
-
$\displaystyle y=f(x,\frac{dy}{dx})$
令 $\displaystyle\frac{dy}{dx}=p$,则方程可参数化 $\begin{cases}x=x\\y'=p\\y=f(x,p)\end{cases}$
把 $y=f(x,p)$ 代入到 $dy=pdx$,得 $\displaystyle\frac{\partial{f}}{\partial{x}}dx+\frac{\partial{f}}{\partial{p}}dp=pdx$,求解之
- 若得到 $p=\varphi(x,c)$,则代回 $y=f(x,p)$ 即得通解
- 若得到 $x=\psi(p,c)$,则通解 $\begin{cases}x=\psi(p,c)\\y=f(\psi(p,c),p)\end{cases}$
- 若得到 $\phi(x,p,c)=0$,则通解 $\begin{cases}\phi(x,p,c)=0\\y=f(x,p)\end{cases}$
-
$\displaystyle x=f(y,\frac{dy}{dx})$
令 $\displaystyle\frac{dy}{dx}=p$,然后两边同时对 $y$ 求导 $\displaystyle\frac{1}{p}=\frac{\partial{f}}{\partial{y}}+\frac{\partial{f}}{\partial{p}}\frac{dp}{dy}$
- 若得到 $p=\varphi(y,c)$,则代回 $x=f(y,p)$ 即得通解
- 若得到 $\phi(y,p,c)=0$,则通解 $\begin{cases}x=f(y,p)\\\phi(y,p,c)=0\end{cases}$
不显含 y 或 x 的方程
-
$F(x,y')=0$
引入变换 $x=\varphi(t)$(或 $y'=\psi(t)$),带入原方程可以得到 $y'=\psi(t)$(或 $x=\varphi(t)$)
$\displaystyle y'=\frac{dy}{dx}\Rightarrow dy=\psi(t)dx=\psi(t)d\varphi(t)=\psi(t)\varphi'(t)dt$
积分之,得到通解 $\begin{cases}x=\varphi(t)\\y=\int\psi(t)\varphi'(t)dt+c\end{cases}$
-
$F(y,y')=0$
引入变换 $y=\varphi(t)$(或 $y'=\psi(t)$),带入原方程可以得到 $y'=\psi(t)$(或 $y=\varphi(t)$)
$\displaystyle y'=\frac{dy}{dx}\Rightarrow dx=\frac{dy}{\psi(t)}=\frac{d\varphi(t)}{\psi(t)}=\frac{\varphi'(t)}{\psi(t)}dt$
积分之,得到通解 $\begin{cases}x=\displaystyle\int\frac{\varphi'(t)}{\psi(t)}dt+c\\y=\varphi(t)\end{cases}$
若 $F(y,0)=0$ 有实根 $y=k$,则 $y=k$ 也是方程的解
第三章 一阶微分方程的解的存在定理
3.1 解的存在唯一性定理与逐步逼近法
利普希茨条件
微分方程 $\displaystyle\frac{dy}{dx}=f(x,y)\ ,R:|x-x_0|\le a\ ,|y-y_0|\le b$
若存在常数 $L>0$ 满足 $|f(x,y_1)-f(x,y_2)|\le L|y_1-y_2|\ ,(x,y_1)\ ,(x,y_2)\in R$
则称 $f(x,y)$ 在 $R$ 上关于 $y$ 满足利普希茨条件,$L$ 称为利普希茨常数
存在唯一性定理 1
若 $f(x,y)$ 在 $R$ 上连续且关于 $y$ 满足利普希茨条件
则方程 $\displaystyle\frac{dy}{dx}=f(x,y)$ 在区间 $|x-x_0|\le h$ 上存在唯一解 $y=\varphi(x)\ ,\varphi(x_0)=y_0$
其中 $\displaystyle h=\min(a,\frac{b}{M})\ ,M=\max_{(x,y)\in R}|f(x,y)|$
存在唯一性定理 2
若 $F(x,y,y')$ 在 $(x_0,y_0,y_0')$ 的某邻域中对 $(x,y,y')$ 连续且存在连续偏导数,同时 $\displaystyle F(x_0,y_0,y_0')=0\ ,\frac{\partial}{\partial{y'}}F(x_0,y_0,y_0')\ne0$
则方程 $F(x,y,y')$ 存在唯一解 $y=\varphi(x)\ ,\varphi(x_0)=y_0\ ,\varphi'(x_0)=y_0'$
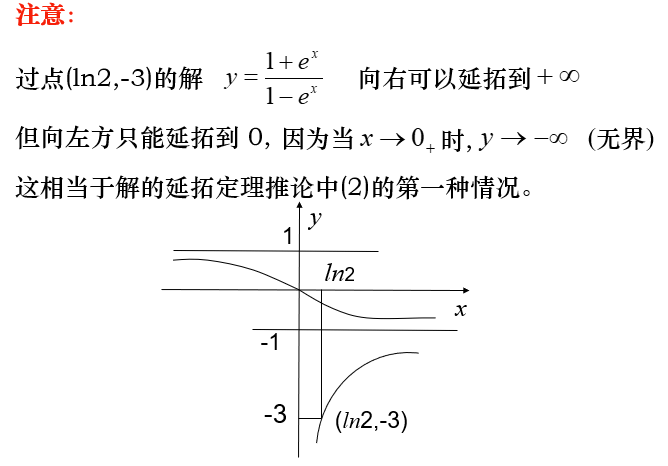
3.2 解的延拓

第四章 高阶微分方程
4.1 线性微分方程的一般理论
基本概念
-
$n$ 阶线性微分方程
- (非齐次)$x^{(n)}+a_1(t)x^{(n-1)}+\cdots+a_{n-1}(t)x'+a_n(t)x=f(t)$
- (齐次)$x^{(n)}+a_1(t)x^{(n-1)}+\cdots+a_{n-1}(t)x'+a_n(t)x=0$
-
朗斯基行列式(函数 $x_i(t)\ (i=1,\cdots,k)$ 在区间 $a\le{t}\le{b}$ 可微 $k-1$ 次)
$W(t)=W[x_1(t),x_2(t),\cdots,x_k(t)]=\left|\begin{array}{c}x_1(t)&x_2(t)&\cdots&x_k(t)\\x_1'(t)&x_2'(t)&\cdots&x_k'(t)\\\vdots&\vdots& &\vdots\\x_1^{(k-1)}(t)&x_2^{(k-1)}(t)&\cdots&x_k^{(k-1)}(t)\end{array}\right|$
-
线性相关
$c_1x_1(t)+c_2x_2(t)+\cdots+c_kx_k(t)\equiv0$($c_i$ 不全为零)
否则称为线性无关
-
基本解组
$n$ 阶齐次线性方程组的一组 $n$ 个线性无关解
齐次线性方程
-
存在唯一性
-
叠加原理:方程的 $k$ 个解的线性组合 $c_1x_1(t)+c_2x_2(t)+\cdots+c_kx_k(t)$ 也是方程的解
-
定理:若函数 $x_1(t),x_2(t),\cdots,x_n(t)$ 在区间 $a\le{t}\le{b}$ 上线性相关(或无关),则该区间上他们的朗斯基行列式恒等于零(或恒不为零)
-
齐次线性方程的基本解组的朗斯基行列式恒不为零
-
通解结构
设齐次线性方程有基本解组 $x_1(t),x_2(t),\cdots,x_n(t)$
则通解可表示为 $x=c_1x_1(t)+c_2x_2(t)+\cdots+c_nx_n(t)$
非齐次线性方程
-
存在唯一性
-
若 $x(t)\ ,\overline{x}(t)$ 分别为“非齐次”与“齐次”的解,则 $x(t)+\overline{x}(t)$ 也是“非齐次”的解
若 $x_1(t)\ ,x_2(t)$ 均为“非齐次”的解,则 $x_1(t)-x_2(t)$ 是“齐次”的解
-
通解结构
设 $x_1(t),x_2(t),\cdots,x_n(t)$ 是“齐次”的一个基本解组,$\overline{x}(t)$ 是“非齐次”的一个特解
则通解 $x=c_1x_1(t)+c_2x_2(t)+\cdots+c_nx_n(t)+\overline{x}(t)$
-
常数变易法
已知“齐次”的一个基本解组 $x_1(t),x_2(t),\cdots,x_n(t)$ 时
$\begin{cases}x_1(t)c_1'(t)+x_2(t)c_2'(t)+\cdots+x_n(t)c_n'(t)=0\\x_1'(t)c_1'(t)+x_2'(t)c_2'(t)+\cdots+x_n'(t)c_n'(t)=0\\\quad\vdots\\x_1^{(n-1)}(t)c_1'(t)+x_2^{(n-1)}(t)c_2'(t)+\cdots+x_n^{(n-1)}(t)c_n'(t)=0\end{cases}$
解出所有 $c_i'(t)$ 并得到 $c_i(t)$ 后可得解 $\displaystyle x=\sum\limits_{i=1}^n\gamma_ix_i(t)+\sum\limits_{i=1}^nx_i(t)c_i(t)$
4.2 常系数线性微分方程
复值函数和复值解
设 $\alpha,\beta$ 为实数,$t$ 为实变量,则 $K=\alpha+i\beta$ 为复数
复指数函数定义为 $e^{Kt}=e^{(\alpha+i\beta)t}=e^{\alpha t}(\cos\beta t+i\sin\beta t)$
$\overline{K}=\alpha-i\beta$ 为 $K$ 的共轭复数,有 $e^{\overline{Kt}}=\overline{e^{Kt}}$

常系数齐次线性方程的特征方程
$L[x]\equiv x^{(n)}+a_1x^{(n-1)}+\cdots+a_{n-1}x'+a_nx=0$ 用 $x=e^{\lambda t}$ 带入
可得到特征方程 $F(\lambda)\equiv\lambda^n+a_1\lambda^{n-1}+\cdots+a_{n-1}\lambda+a_n=0$
-
$\lambda$ 为 $k$ 重实根时,方程有 $k$ 个解 $t^je^{\lambda t}\ (j=0,1,2,\cdots,k-1)$
$e^{\lambda t},te^{\lambda t},t^2e^{\lambda t},\cdots,t^{k-1}e^{\lambda t}$
-
$\lambda=\alpha\pm i\beta$ 为 $k/2$ 重共轭复根时,方程有 $k/2$ 对共轭复值解,也就是一共 $k$ 个复值解
每对为 $t^je^{\alpha t}\cos\beta t,t^je^{\alpha t}\sin\beta t\ (j=0,1,2,\cdots,k/2-1)$
得到基本解组 $x_1,x_2,\cdots,x_k$ 后,可写出通解 $x(t)=c_1x_1+c_2x_2+\cdots+c_kx_k$
欧拉方程
对于欧拉方程 $x^ny^{(n)}+a_1x^{n-1}y^{(n-1)}+\cdots+a_{n-1}xy'+a_ny=0$
核心思想:引进自变量变换 $x=e^t$ 或 $t=\ln|x|$ 可化为常系数齐次线性微分方程 $y^{(n)}+b_1y^{(n-1)}+\cdots+b_{n-1}y'+b_ny=0$
解法:
-
求特征方程 $F(k)$ 的特征根
$F(k)=k(k-1)\cdots(k-n+1)+a_1k(k-1)\cdots(k-n+2)+\cdots+a_{n-1}k+a_n$
-
得到基本解组,然后使用 $t=\ln|x|$ 变换得到原方程的基本解组
- 得到原方程通解
常系数非齐次线性方程的比较系数法
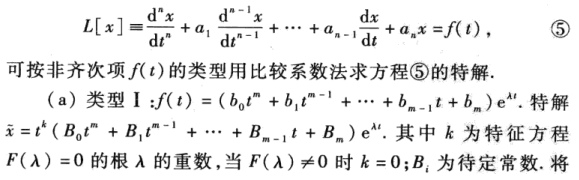

4.3 高阶方程降阶法
可降阶
-
方程不含未知函数 $x$,形如 $F(t,x^{(k)},x^{(k+1)},\cdots,x^{(n)})=0\ (1\le k\le n)$,则令 $y=x^{(k)}$,可降 $k$ 阶
求得降阶后方程的通解后,逐次积分 $k$ 次即可得到原方程通解
-
方程不含自变量 $t$,形如 $F(x,x',\cdots,x^{(n)})=0$,令 $y=x'$,可降低1阶
$\displaystyle x^{(n)}=y^{n-1}\frac{d^{n-1}y}{dx^{n-1}}$ 全部带入原方程,分离变量,可得原方程解
-
齐次线性方程已知 $k$ 个线性无关的非零特解 $x_1,x_2,\cdots,x_k$,可降低 $k$ 阶
-
特别地,对于二阶齐次线性方程 $x''+p(t)x'+q(t)x=0$,已知非零特解 $x_1$
通解为 $\displaystyle x=x_1[c_1+c_2\int{\frac{1}{x_1^2}e^{-\int{p(t)}dt}}dt]$
-
二阶线性方程的幂级数解(求特解)
看不懂,这分我不要了(
第五章 线性微分方程组
5.1 存在唯一性定理
$\begin{cases}x_1'=a_{11}(t)x_1+a_{12}(t)x_2+\cdots+a_{1n}(t)x_n+f_1(t)\\x_2'=a_{21}(t)x_1+a_{22}(t)x_2+\cdots+a_{2n}(t)x_n+f_2(t)\\\quad\vdots\\x_n'=a_{n1}(t)x_1+a_{n2}(t)x_2+\cdots+a_{nn}(t)x_n+f_n(t)\end{cases}$
$n$ 阶线性微分方程组:$\boldsymbol{x}'=\boldsymbol{A}(t)\boldsymbol{x}+\boldsymbol{f}(t)$
$\boldsymbol{x}=(x_1,x_2,\cdots,x_n)^T\ ,\boldsymbol{A}(t)=[a_{ij}(t)]\ ,\boldsymbol{f}(t)=(f_1(t),f_2(t),\cdots,f_n(t))^T$
初值问题:$\boldsymbol{x}(t_0)=\boldsymbol{\eta}$
$x^{(n)}+a_1(t)x^{(n-1)}+\cdots+a_{n-1}x'+a_n(t)x=f(t)$
$x(t_0)=\eta_1,x'(t_0)=\eta_2,\cdots,x^{(n-1)}(t_0)=\eta_n$
5.2 一般理论
基本概念
$\displaystyle\frac{d\boldsymbol{x}}{dt}=\boldsymbol{x}'=\boldsymbol{A}(t)\boldsymbol{x}+\boldsymbol{f}(t)$
-
如果 $\boldsymbol{f}(t)\ne0$ 则为非齐次线性的,$\boldsymbol{f}(t)\equiv0$ 则为齐次线性的
若 $\boldsymbol{A}(t)$ 为常数矩阵,则称为常系数线性方程组
$\boldsymbol{x}'=\boldsymbol{A}(t)\boldsymbol{x}\ \Rightarrow\ \boldsymbol{x}'=\boldsymbol{A}\boldsymbol{x}$
-
线性相关
$c_1\boldsymbol x_1(t)+c_2\boldsymbol x_2(t)+\cdots+c_m\boldsymbol x_m(t)\equiv0$($c_m$ 不全为零)
否则它们(向量函数)线性无关
-
基本解组
$n$ 维一阶齐次线性方程组的一组 $n$ 个线性无关解 $\boldsymbol x_1(t),\boldsymbol x_2(t),\cdots,\boldsymbol x_n(t)$ 组成的矩阵 $\boldsymbol\phi(t)$
当 $\boldsymbol\phi(0)=\boldsymbol E$(单位矩阵)时称基本解组为标准的
齐次线性方程组
$\boldsymbol{x}'=\boldsymbol{A}(t)\boldsymbol{x}$
-
存在唯一性
-
叠加原理
方程组的 $k$ 个解 $\boldsymbol x_1(t),\boldsymbol x_2(t),\cdots,\boldsymbol x_k(t)$ 的线性组合 $c_1\boldsymbol x_1(t)+c_2\boldsymbol x_2(t)+\cdots+c_k\boldsymbol x_k(t)$ 也是方程的解,其中 $c_i$ 为任意常数
-
如果向量函数 $\boldsymbol x_1(t),\boldsymbol x_2(t),\cdots,\boldsymbol x_n(t)$ 在某区间上线性相关(或无关),则他们的朗斯基行列式恒为零(或恒不为零)
齐次线性方程组的基本解组的朗斯基行列式恒不为零
-
通解结构
设 $\boldsymbol\phi(t)$ 是齐次线性方程组的一个基本解组,则通解可以表示为
$\boldsymbol{x}=\boldsymbol{\phi}(t)\boldsymbol{c}\equiv c_1\boldsymbol x_1(t)+c_2\boldsymbol x_2(t)+\cdots+c_n\boldsymbol x_n(t)$
其中 $\boldsymbol{c}=(c_1,c_2,\cdots,c_n)^T$ 为任意常向量
-
齐次线性方程组的 $n$ 个解 $\boldsymbol x_1(t),\boldsymbol x_2(t),\cdots,\boldsymbol x_n(t)$ 组成基本解组 $\boldsymbol\phi(t)$ 的充要条件为 $\det\boldsymbol\phi(t)\ne0$
齐次线性方程组的两个基本解组 $\boldsymbol\phi(t),\boldsymbol\psi(t)$ 必有关系
$\boldsymbol\phi(t)=\boldsymbol\psi(t)\boldsymbol C\ (a\le t\le b)\ ,\det\boldsymbol C\ne0$
非齐次线性方程组
-
存在唯一性
-
若 $\boldsymbol x(t)\ ,\widetilde{\boldsymbol x}(t)$ 分别为“非齐次”与“齐次”的解,则 $\boldsymbol x(t)+\widetilde{\boldsymbol x}(t)$ 也是“非齐次”的解
若 $\boldsymbol x_1(t)\ ,\boldsymbol x_2(t)$ 均为“非齐次”的解,则 $\boldsymbol x_1(t)-\boldsymbol x_2(t)$ 是“齐次”的解
-
通解结构
设 $\boldsymbol{\phi}(t)$ 是“齐次”的一个基本解组,$\widetilde{\boldsymbol x}(t)$ 是“非齐次”的某一特解,则通解可表示为
$\boldsymbol{x}=\boldsymbol{\phi}(t)\boldsymbol{c}+\widetilde{\boldsymbol x}(t)$ 其中 $\boldsymbol{c}$ 为任意 $n$ 维向量
- 常数变易法
5.3 常系数线性微分方程组
看不懂,这分我不要了 QAQ
版权声明:本文为原创文章,版权归 神代綺凜 所有。
本文链接:https://moe.best/gotagota/ode.html
所有原创文章采用 知识共享署名-非商业性使用 4.0 国际许可协议 进行许可。
您可以自由的转载和修改,但请务必注明文章来源并且不可用于商业目的。
----- 一枚00后